5 Keys to Campaign Strategy #5: High-Variance Plays
When it’s better to use strategies that are normally worse

For the final installment in this series, I’d like to turn to an especially topical subject: how campaigns strategize at the very end of election seasons.
In the last few weeks of an election, time and money are more scarce than ever, and each decision is pivotal. That’s why the end of the campaign season is the most strategically-interesting part, like how the last five minutes are the most interesting part of any pro sports game.
The current US Presidential election is in a quite interesting strategic place, so let’s use that as our jumping-off point for this piece.
Suppose you’re Donald Trump and you’re far behind in the polls, hoping to pull a rabbit out of a hat and win a second term. Where do you focus your resources? Do you try to shore up support in normally-red states that might flip, like Georgia or Texas? Or do you go more on offense, trying to claw back states like Michigan and Pennsylvania, which have lurched toward your opponent’s corner?
High- and low-variance strategies
Here’s a more general way to think about Trump’s two options. He can either:
- Try to lock down safer states while giving up on more iffy states: a defensive play.
- Try to make iffy states competitive again while betting that you can carry safer states without any investment: an offensive play.
Playing defensively would effectively decrease the number of competitive states, since he’d make light-red states dark red and let light-blue states become dark blue. Thus, Trump would have a low probability of getting a landslide win or a landslide loss; he’d be much more likely to get a moderate result. If we plotted his possible Electoral College outcomes with a Bell curve, he’d have a high peak with narrow tails, representing low variance in the possible outcomes:
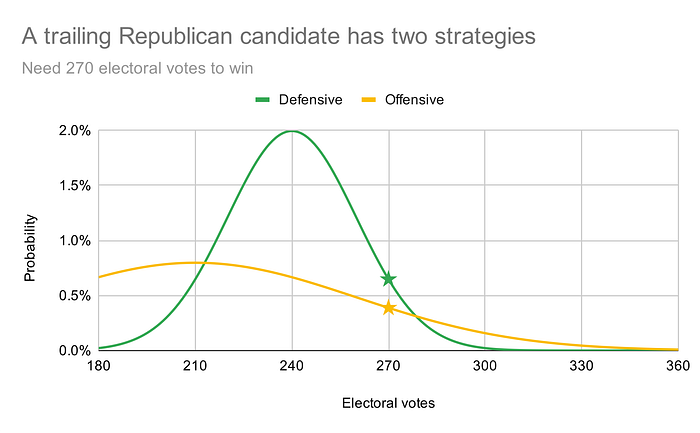
On the flip side, playing offensively would make more states competitive. Trump would drag states like MI and PA toward toss-up territory, but he’d also let places like NC and TX drift toward toss-up status too. His outcomes would be high variance: with so many states becoming coin flips, the odds of landslides in either direction would be quite high. Thus, this strategy’s Bell curve would have a lower peak and much fatter tails. And because Trump would now risk losing places like Texas, he’d average fewer electoral votes than in the defensive strategy: the peak would be further to the left on our graph.
Going on offense is a high-variance strategy; going on defense is low-variance.
At first glance, it seems like the defensive strategy is best, since the average outcome is better for Trump. In our graph, Trump gets an average of 240 electoral votes if he plays defense but just 210 if he plays offense.
But looking at the average outcomes is wrong in this instance. That’s because elections are an unusual type of game, and you have to understand this type of game to understand how to compare the various strategies.
Three types of games
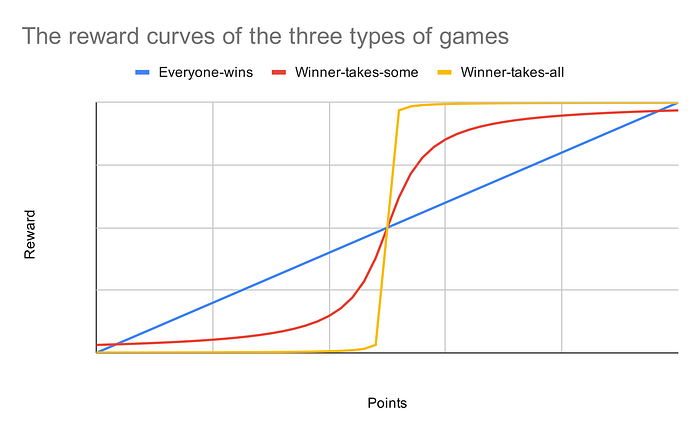
So, what is a game? Let’s define a “game” as a challenge where you earn a certain number of points (the input) and are awarded a certain amount of reward (the output). The more apples you pick, the more apple pies you can bake. The more runs you score in a baseball game, the better your chance of victory, and thus the better your win-loss record. At work, the more effort you put in, the more money you get out (hopefully).
Note, though, that the correlation between points and rewards isn’t always smooth. Sometimes, games have thresholds or discontinuities, above which your rewards can suddenly change. Going from 21 to 22 in blackjack turns a big payday into a “bust;” going from 268 to 270 electoral votes suddenly takes you from losing to becoming President. We can group games into three buckets based on the types of thresholds they have.
Everyone-wins
First are simple everyone-wins games, which have no thresholds. Getting more points is always a good thing; putting in more effort always pays off. Some examples:
- Earning money: nobody would say no to an extra $10.
- Running a 10K: there’s no particular time you have to hit (unless you’ve set a goal for yourself), so shaving time off your run is always advantageous.
- Posting on Facebook: there’s no “magic number” of likes you have to get; the more likes, the better.
In all these examples, the relationship between points and rewards is a smooth line.
Winner-takes-all
On the other end of the spectrum are winner-take-all games, which have sharply binary outcomes around a threshold. If you pass the threshold, you’ll win, whether you win in a rout or eke out a victory. If you fall short, you’ll lose, no matter how close you got. Some examples:
- Sports is the obvious one. Whether your team lost 28–27 or 28–0, they’ll still get one more in the loss column.
- If you need 60% to pass an exam, going from 59% to 60% makes a huge difference. Improving your score from 30% to 50%, meanwhile, won’t help you one bit.
- Elections are the other classic example. You just need 1 more vote than your opponent to win; getting 5 million more votes is nice but ultimately inconsequential.
As you can see, wild swings can happen at the thresholds. It’s not usually a big deal if you lose two votes… except if you go from winning by one vote to losing by one vote.
Winner-takes-some
The last type of game falls somewhere in the middle: there’s a sharp jump around a threshold, but it’s still valuable to get additional points. It’s not binary, but it’s not perfectly smooth either. These winner-takes-some games are rare, but fortunately, elections provide a great example.
Consider the US House of Representatives, where a party needs 218 seats out of 435 to win control of the chamber. There’s a big difference between controlling 217 seats and 218: you flip from the minority party to the majority party, take control of key committees, and so on.
But it’s still valuable to get seats beyond the 218th. Controlling 230 seats, for instance, is even better, since you can afford to let a dozen members of your coalition defect and still be able to pass legislation.
Variance in winner-take-all games
Unlike the House, however, the Electoral College is a starkly winner-takes-all game. Whether you win 400 electoral votes or 280, you’re still President. More importantly for Donald Trump, increasing your electoral vote haul from 210 to 240 does you zero favors.
Go high-variance if you’re losing
I chose those numbers for a reason. Recall Trump’s options: he can use a defensive strategy that averages him 240 electoral votes or an offensive strategy that averages him 210 electoral votes. In an everyone-wins game, the strategy with the higher average score would be better, but in this winner-takes-all game, the average score is entirely irrelevant. Instead, all Trump should care about is his odds of getting 270+ electoral votes.
Going back to the graph, Trump should pick the strategy that maximizes the area under the curve to the right of 270; this represents his total probability of winning the Electoral College.

In our example, the area under the offensive (yellow) curve to the right of 270 is 12%, indicating that Trump should be expected to get 270 or more electoral votes 12% of the time. Meanwhile, the area under the defensive (green) curve to the left of 270 is just 7%, giving Trump just a 7% chance of victory. (This might seem strange, since the green curve is higher than the yellow curve at 270, but the yellow curve’s fat tails add a lot of area.)
So the offensive, high-variance strategy is expected to help Trump prevail 12% of the time, while the defensive, low-variance strategy gives him odds of just 7%. The high-variance strategy is clearly Trump’s best bet.
Interestingly enough, the high-variance strategy gives Trump better odds despite its average outcome being worse! In other words, the outcome that would be worse in an everyone-wins game is actually the better outcome in this winner-take-all game.
Thus this general wisdom:
If you’re losing a winner-take-all game, you need to use a high-variance strategy. You risk a blowout loss, but it’s the only way to give yourself a shot at winning. A low-variance play will only cement a narrow loss for you.
The key thing to realize is that a narrow loss is no better than a blowout loss. You’re thus free to take aggressive risks — in fact, that’s probably your only way to carve out a plausible path to victory. This is why football teams that are down 15 points in the last few minutes will throw fifty-yard “Hail Mary” passes: they aren’t likely to succeed, and in all likelihood they’ll just get intercepted, but what other option does the team have?
Practically speaking, this means that Trump needs to ignore states like North Carolina and Texas, gambling that they’ll stick with him, and instead focus his attention on the bluer swing states like Michigan and Wisconsin. Trying to lock down Texas might cut his Electoral College losses, but if he gives up on places like Michigan, he’s going to lose the election no matter what.
Go low-variance if you’re winning
The complete opposite guidance applies if you’re winning a winner-takes-all game: minimize variance, lock down your path to victory, and cut off your opponent’s path to an upset. If you’re sitting at 300 electoral votes, there’s no benefit (besides bragging rights) to getting up to 360, so don’t get greedy.
For Joe Biden, who’s currently enjoying a hefty polling lead, this means that he should pursue defensive, lower-variance strategies. In response to Trump’s Hail Marys, Biden should be “taking a knee” as he runs down the clock.

This means that Biden shouldn’t be spending much time in offensive targets like Texas or Georgia; instead, he should be focusing on locking down places like Pennsylvania and Michigan. He wants to put as many states as possible into the blue column, even if that means deprioritizing the toss-ups.
Interestingly enough, this means that both Trump and Biden should be spending time in the same upper Midwestern swing states… but for opposite reasons! Biden’s defensive targets are Trump’s offensive targets, and vice versa.
Game theory
Now, there’s plenty of meta-strategy that campaigns can (and do) layer on top of this. For instance, as I’m writing this, Kamala Harris is campaigning in Texas. Our variance analysis shows that her campaign doesn’t need to spend time here, so why is she doing it?
I’d argue that this is a “fake-out.” By campaigning in Texas, Harris is trying to trick Trump into getting scared and spending his few remaining days in Texas when he should really be focusing on the Midwest. She’s trying to bait Trump into following the strategy that could seal his defeat.
Biden, meanwhile, is spending quality time in Pennsylvania. He’s playing defense as he should while letting his second-in-command distract Trump. This shows the Biden/Harris campaign’s strong grasp of strategy: they know the plays they should be making and the plays Trump’s campaign should be making, and they’re executing their plays while drawing Trump away from his.
The end (for now)
I hope you’ve enjoyed this article and this series, and that you’re walking away a savvier politician, a smarter campaign worker, or a better-informed citizen. I know I’ve certainly enjoyed drawing together the disparate fields of economics, statistics, optimization, game theory, and math to develop a deeper understanding of campaign strategy.
That’s a wrap for this series, but feel free to let me know in the comments, on Twitter, or on LinkedIn if you’d like to see more analysis like this.
And, above all else, remember:
